Imputation
Motivation
Imputation is often required in DNAm studies, such as to ensure phenotype predictors have access to complete unbiased data or for algorithms that cannot accept NA values like SVA. Various options are available, including:
impute.knnfrom impute, a package for imputation of microarray data- missForest, which imputes data using random forests, and
- methyLImp220, which is specifically designed for DNAm data
Although in-depth benchmarking is yet to be completed, we outline the use of methyLImp2 for imputation to create a complete matrix of beta values.
Of note, EPICv2 CpGs have technical suffixes for CpG names, which predictors may not be updated for. Additionally, CpGs have up to 10 replicates. We advise selecting one of these at random to use in prediction, or selecting the one with the best performing detection p-value, which can be inspected using detectionP() from minfi.
methyLImp2
The main function methyLImp2 can take a SummarizedExperiment or beta matrix as input, and requires the array type to be specified (as 450k or EPIC). By default it will overwrite your SummarizedExperiment object.
## used (Mb) gc trigger (Mb) max used (Mb)
## Ncells 23346621 1246.9 38694734 2066.6 38694734 2066.6
## Vcells 2876341126 21944.8 8625936037 65810.7 10781960631 82259.9methData <- methyLImp2(
input = methData,
type = "EPIC",
BPPARAM = MulticoreParam(workers = nworkers, progressbar = TRUE),
minibatch_frac = 0.5)## | | | 0% | |=== | 5% | |====== | 9% | |========== | 14% | |============= | 18% | |================ | 23% | |=================== | 27% | |====================== | 32% | |========================= | 36% | |============================= | 41% | |================================ | 45% | |=================================== | 50% | |====================================== | 55% | |========================================= | 59% | |============================================= | 64% | |================================================ | 68% | |=================================================== | 73% | |====================================================== | 77% | |========================================================= | 82% | |============================================================ | 86% | |================================================================ | 91% | |=================================================================== | 95% | |======================================================================| 100%We can extract betas for use in our predictors, and reduce precision as described earlier.
Covariates
Calculate PCs
Principal components (PCs) of the beta values can be calculated using prcomp as before to investigate variables important to adjust for in the EWAS analysis.
Heatmap
Each column in the RGset colData should be considered as a potential covariate in EWAS models. Both technical and biological factors should be investigated as these may introduce batch effects or be clinically relevant. In order to assess this, you can visualize correlations with PCs as done previously in this workflow.
Any constant variables are removed from the heatmap, as they will not explain variance in the data.
plot_vars <- apply(targets, 2, function(x) sd(as.numeric(factor(x)), na.rm=T))
plot_vars <- names(plot_vars[!plot_vars %in% c(NA, 0)])
plot_vars## [1] "sample_ID" "geo_accession" "sex"
## [4] "age" "log_total_pbb" "pbb_153"
## [7] "pbb_77" "pbb_101" "pbb_180"
## [10] "supplementary_file" "plate" "row"
## [13] "Basename" "CD4Tnv" "Baso"
## [16] "CD4Tmem" "Bmem" "Bnv"
## [19] "Treg" "CD8Tmem" "CD8Tnv"
## [22] "Eos" "NK" "Neu"
## [25] "Mono"All variables are then converted to numeric and correlations between them and the PCs are calculated.
heatmap_df <- apply(heatmap_df, 2, function(x) as.numeric(factor(x)))
cxy <- round(cor(pca$x, scale(heatmap_df), use="pairwise.complete.obs"),2) A heatmap can then be used to visualize these correlations and uncover measured variables that explain a large proportion of DNAm variance.
col_fun <- colorRamp2(c(-1, 0, 1), c("#000042", "white", "#800000"))
Heatmap(
t(cxy),
col = col_fun,
border = 'grey5',
cluster_columns = FALSE,
show_row_dend = TRUE,
show_column_dend = FALSE,
name = "Value",
row_names_gp = gpar(fontsize = 8),
column_names_gp = gpar(fontsize = 8),
cell_fun = function(j, i, x, y, width, height, fill) {
grid.rect(x, y, width, height,
gp = gpar(col = "white", lwd = 1, fill = NA))
grid.text(ifelse(abs(t(cxy)[i,j]) > 0.4,
sprintf("%.2f", round(t(cxy)[i, j], 2)),
""),
x, y, gp = gpar(fontsize = 8, col = "white"))
}
)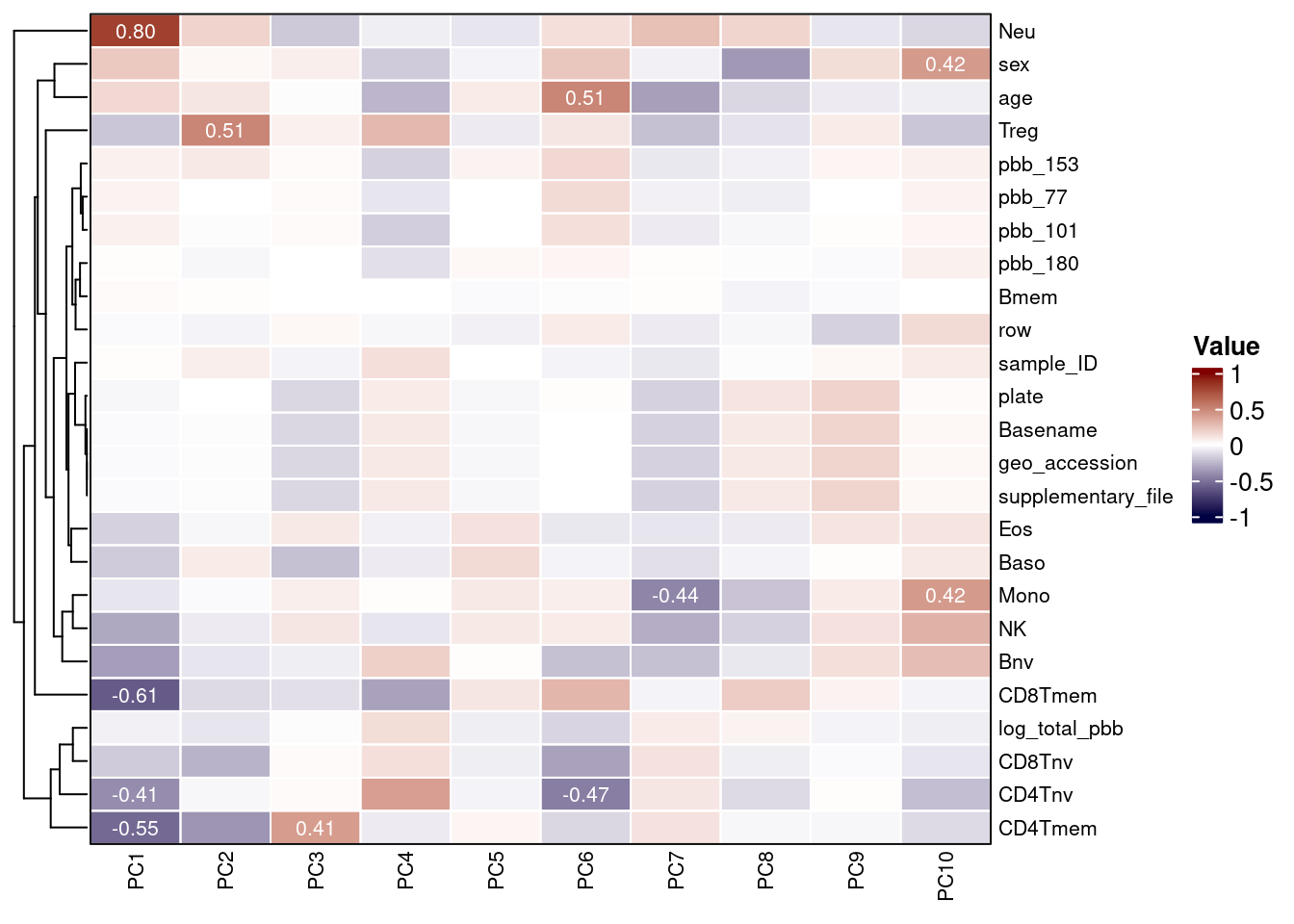
By examining the correlations in the data, we can build our model in a more informed manner. The second PC is highly correlated with sex and, as is usual in EWAS, we intend to include this as a confounder.
Some predicted cell counts appear of substantial importance and we advise also adjusting for these. Model specification should be informed by a combination of prior knowledge and inspection of patterns in the data.
SVA
Motivation
The sva package contains functions for removing batch effects and other unwanted variation in high-throughput experiments. Specifically, the sva package contains functions for the identifying and building surrogate variables for high-dimensional data sets. Surrogate variables are covariates constructed directly from high-dimensional data (like DNAm data) that can be used in subsequent analyses to adjust for unknown, unmodeled, or latent sources of noise.
The sva package can be used to remove artifacts in three ways:
- identifying and estimating surrogate variables for unknown sources of variation in high-throughput experiments23
- directly removing known batch effects using ComBat24, and
- removing batch effects with known control probes25
Removing batch effects and using surrogate variables in differential expression analysis have been shown to reduce dependence, stabilize error rate estimates, and improve reproducibility23,26. In addition to SVA, the cate package provides a related framework that also estimates latent factors to account for unobserved confounders in high-dimensional data, and was previously the standard approach in epigenome-wide pipelines.
Specification
The full model and null model are specified with and without the variable of interest respectively. In this case, we adjust for sex, age, plate, row, CD4Tnv, Baso, CD4Tmem, Bmem, Bnv, Treg, CD8Tmem, CD8Tnv, Eos, NK, and Mono. Neutrophils are excluded to avoid collinearity as all predicted cell counts sum to 1.
mod = model.matrix(~log_total_pbb + age + sex + plate + row + CD4Tnv + Baso + CD4Tmem + Bmem + Bnv + Treg + CD8Tmem + CD8Tnv + Eos + NK + Mono, data=targets)
mod0 = model.matrix(~age + sex + plate + row + CD4Tnv + Baso + CD4Tmem + Bmem + Bnv + Treg + CD8Tmem + CD8Tnv + Eos + NK + Mono,data=targets)Latent factor calculation
This can then be used to estimate the appropriate number of latent factors to calculate.
The latent factors can then be calculated with the sva function:
These can then be added to targets to include in the EWAS model.
sv_df <- as.data.frame(svobj$sv)
colnames(sv_df) <- c('SV1', 'SV2', 'SV3', 'SV4')
targets <- cbind(targets, sv_df)EWAS
Packages
Limma27 is a package with excellent documentation that can be useful for smaller samples, due to the optional empirical Bayes step. Other packages that may be of interest for running EWAS include gee and cate.
Formula
In order to run an EWAS a formula needs to be specified based on the above exploratory analyses and SVA.
You can then use this formula to create a design matrix.
## (Intercept) log_total_pbb age sexMale
## GSM3228563_200550980002_R02C01 1 -2.7535707 31.46 0
## GSM3228564_200550980002_R03C01 1 -0.3714986 46.72 1
## plate200550980010 plate200550980025
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200550980034 plate200550980035
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200590490002 plate200590490017
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200590490021 plate200590490052
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200590490056 plate200590490062
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200590490074 plate200590500076
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200594720026 plate200594720075
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200594720089 plate200594740031
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200594740033 plate200594740034
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200594740035 plate200594740039
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200594740046 plate200594740047
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200594740051 plate200594740052
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200594740057 plate200594740069
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200594740070 plate200594740072
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200594740073 plate200594740075
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200594740079 plate200594740080
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200594740083 plate200594740084
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200594740085 plate200594740086
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200594740087 plate200594740089
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200598340032 plate200598340033
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200598340037 plate200598340040
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200598350004 plate200598350005
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200598350006 plate200598350011
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200598350012 plate200598350015
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200598350017 plate200598350018
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200598350022 plate200598350025
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200598350027 plate200598350029
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200598350041 plate200598350042
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200598350043 plate200598350044
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200598350045 plate200598350052
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200598350053 plate200598350054
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200598350062 plate200598350065
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200598350066 plate200598350067
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200598350069 plate200598350075
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200598350076 plate200598350077
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200598350078 plate200598350079
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200598350080 plate200598360001
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200598360002 plate200598360003
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200598360004 plate200598360005
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200598360006 plate200598360007
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200598360008 plate200598360014
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200598360025 plate200598360026
## GSM3228563_200550980002_R02C01 0 0
## GSM3228564_200550980002_R03C01 0 0
## plate200598360027 row CD4Tnv Baso
## GSM3228563_200550980002_R02C01 0 2 0.11996132 0.00000000
## GSM3228564_200550980002_R03C01 0 3 0.05616825 0.00408646
## CD4Tmem Bmem Bnv Treg
## GSM3228563_200550980002_R02C01 0.07081197 0.04298515 0.00000000 0.02895521
## GSM3228564_200550980002_R03C01 0.06505466 0.03205729 0.03627479 0.03253338
## CD8Tmem CD8Tnv Eos NK
## GSM3228563_200550980002_R02C01 0.05436260 0.06774525 0.002143475 0.03400832
## GSM3228564_200550980002_R03C01 0.02641348 0.00000000 0.013666271 0.06104596
## Mono
## GSM3228563_200550980002_R02C01 0.0832361
## GSM3228564_200550980002_R03C01 0.1756234Random effects
Random effects can be included using duplicateCorrelation and specifying the block argument. This is useful for paired experiments, not used in this example, but with example code shown here.
Fitting models
Models are fit using lmFit.
Models can also be fit for random effects using the dupcor object created above.
fit <- lmFit(betas, design,
block = colData(methData)$ID,
correlation = dupcor$consensus.correlation)Extracting results
Results can then be extracted from the fit object, including the:
- coefficients
coef - standard errors
se - t-statistics
tstat - p-values
pval, and - number of observations
n
coef <- fit$coefficients[, 2]
se <- fit$stdev.unscaled[, 2] * fit$sigma
tstat <- coef / se
pval <- 2 * pt(-abs(tstat), fit$df.residual)
n <- ncol(design) + fit$df.residualbacon
Motivation
We developed a package called bacon11 to estimate and correct for bias and inflation of test statistics in EWAS. This maximizes power while properly controlling the false positive rate, by estimating the empirical null distribution using Bayesian statistics. The utility of the tool was illustrated through the application of meta-analysis by performing epigenome- and transcriptome-wide association studies (EWASs/TWAS) on age and smoking which highlighted an overlap in differential methylation and expression of associated genes. However, it is important to note that this approach may not work well on smaller datasets and diagnostic plots are essential when applied in this setting (i.e. fewer than 200 samples).
Adjusting for bias and inflation
We advise using bacon to estimate inflation and bias often observed in EWAS. This object can then be printed to report the estimated bias and inflation.
## Use multinomial weighted sampling...## threshold = -5.3980
## Starting values:
## p0 = 1.0000, p1 = 0.0000, p2 = 0.0000
## mu0 = -0.2161, mu1 = 5.3589, mu2 = -5.7911
## sigma0 = 1.0328, sigma1 = 1.0328, sigma2 = 1.0328## Bacon-object containing 1 set(s) of 743324 test-statistics.
## ...estimated bias: -0.071.
## ...estimated inflation: 0.94.
##
## Empirical null estimates are based on 5000 iterations with a burnin-period of 2000.P-values and t-statistics can then be adjusted
Plots
Bacon also provides some visualizations of its performance, which can come in handy. In addition to inspecting diagnostic plots using traces, posteriors, and fit, checking the QQ plots as shown below is an essential step.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.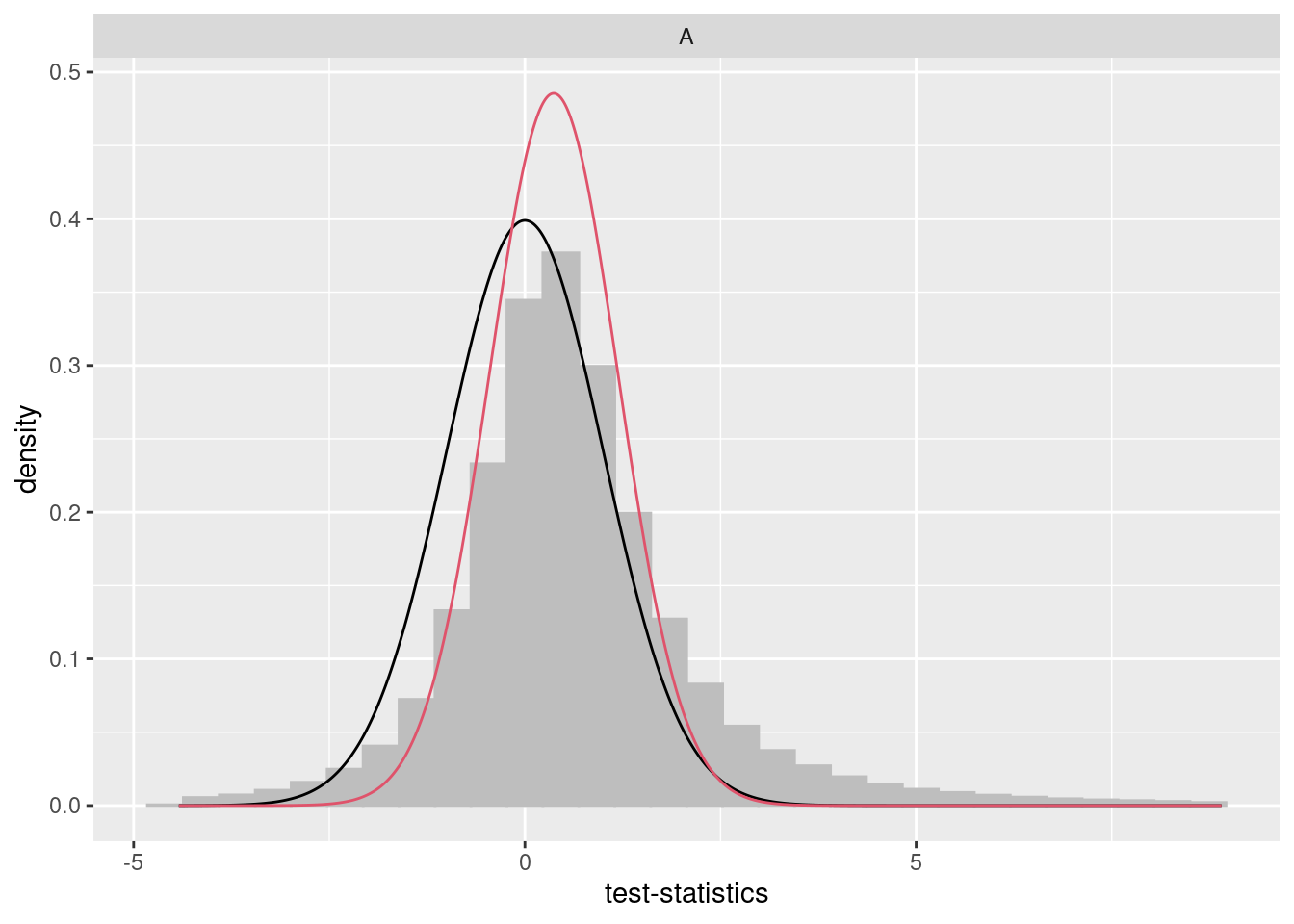
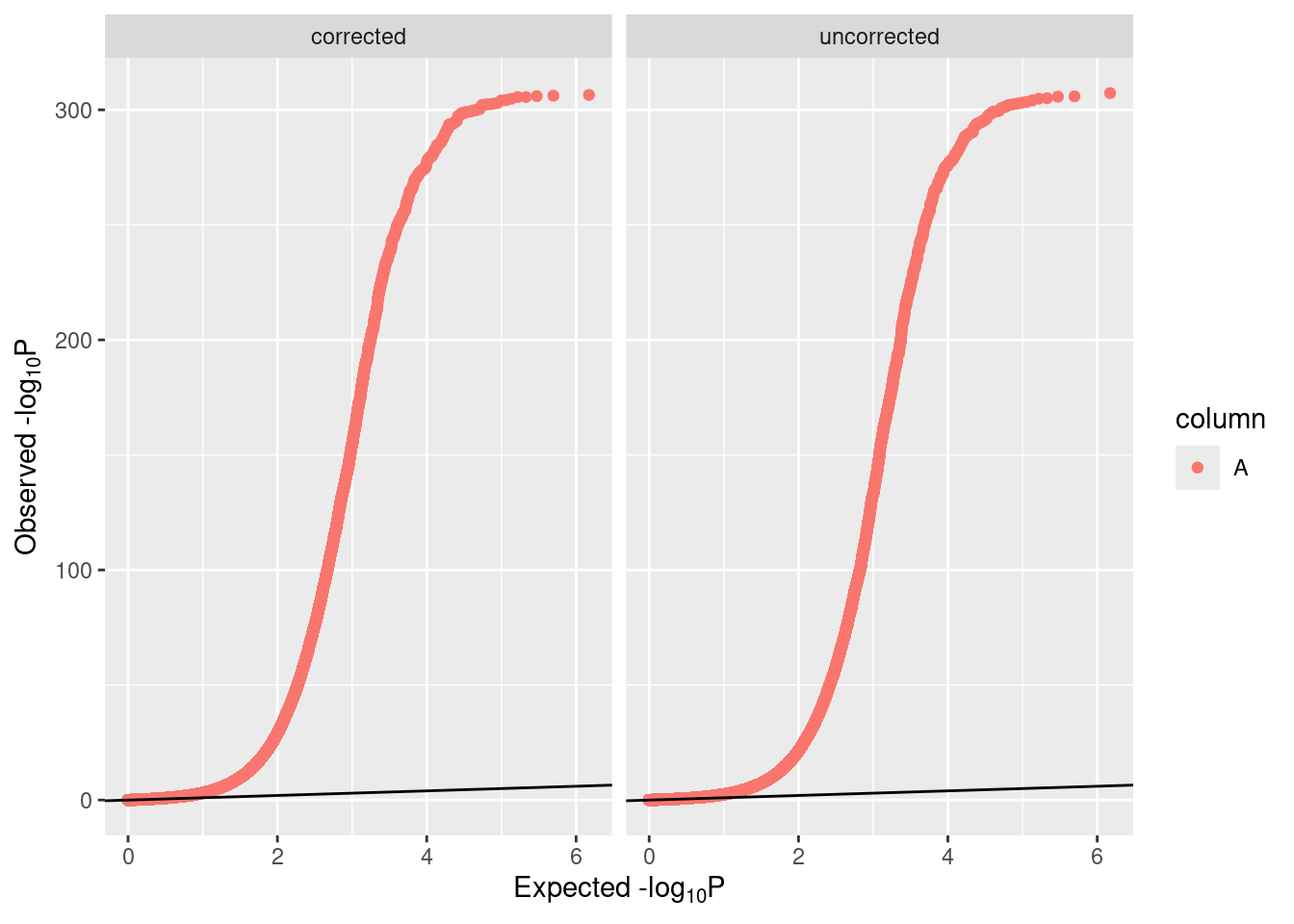
Additionally, rerunning bacon can provide an estimate of any residual bias or inflation.
## Use multinomial weighted sampling...## threshold = -5.3980
## Starting values:
## p0 = 1.0000, p1 = 0.0000, p2 = 0.0000
## mu0 = -0.1549, mu1 = 5.8058, mu2 = -6.1157
## sigma0 = 1.1043, sigma1 = 1.1043, sigma2 = 1.1043## Bacon-object containing 1 set(s) of 743324 test-statistics.
## ...estimated bias: 0.007.
## ...estimated inflation: 1.
##
## Empirical null estimates are based on 5000 iterations with a burnin-period of 2000.Saving results
Bacon-adjusted results can then be saved, for use in downstream analysis.
limma_base <- data.frame(cpg = rownames(fit$coefficients),
beta = coef, SE = se,
p = pval,
t = tstat, N = n)